Notes from Chaudhury, et al. (2024), chapter 3
New highlights added June 19, 2024 at 4:30 PM
- The answer is yes. A matrix can always be converted into a vector by a process called rasterization. (View Highlight)
- Note: The author is actually confused. Rasterization is the process of converting a vector to a bitmap (“raster”); vectorization is the process of converting a bitmap to a vector.
- rasterization (View Highlight)
- Note: vectorization
- rasterized vector (View Highlight)
- Note: vector
- matrix (View Highlight)
- Note: raster
- rasterization (View Highlight)
- Note: vectorization
- In the special case of binary classifiers, the sign of the expression 휙 x; w, b representing the decision boundary has a special significance. (View Highlight)
- in binary classification, once we have estimated an optimal decision surface 휙 sign of 휙 x; w, b x; w, b , given any input vector x, we can compute the to predict the class. (View Highlight)
- if we are describing a continuous (smooth) function in the neighborhood of a specific point, we use a Taylor series. A Taylor series allows us to describe a function in the neighborhood of a specific point in terms of the value of the function and its derivatives at that point. (View Highlight)
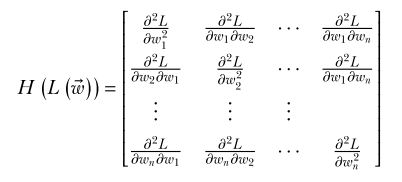
- In equation 3.7, we express a function of one variable in a small neighborhood around a point in terms of the derivatives. Can we do a similar thing in higher dimensions? Yes. We simply need to replace the first derivative with the gradient. We replace the second derivative with its multidimensional counterpart: the Hessian matrix. (View Highlight)
(View Highlight)
- Note: Hessian matrix. Replaces the derivative in the multidimensional version of the Taylor series.
- A convex surface (see figure 3.14) has a single optimum (maximum/minimum): the global one.2 (View Highlight)
- , a set of points is said to be convex if and only if the straight line joining any pair of points in the set lies entirely within the set. (View Highlight)
- a set of points is nonconvex if it contains at least one pair of points whose joining line contains a point not belonging to the set. (View Highlight)
- we know that all points C on L can be expressed as a weighted average of the coordinates of A and B, with the sum of weights being 1. Thus, C ≡ (훼1x1 + 훼2x2, 훼1y1 + 훼2y2), where 훼1 + 훼2 = 1. (View Highlight)
- if we drop a perpendicular to the X-axis from any point on the secant line joining a pair of points on the curve, that perpendicular will cut the curve at a lower point (that is, smaller in its Y-coordinate). (View Highlight)
(View Highlight)
- Note: First definition of convexity
- convex curves always curl upward and/or rightward everywhere. This leads to another equivalent definition of convexity. (View Highlight)
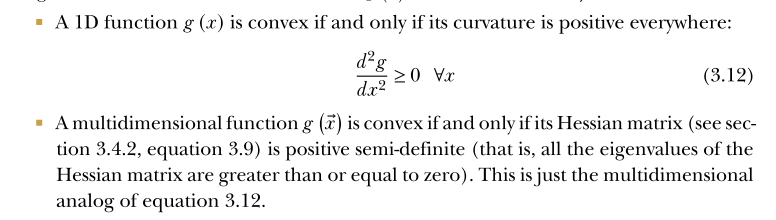?t=1718828586417 (View Highlight)
- Note: Second definition of convexity
- t if the second derivative is negative everywhere or the Hessian is negative semi-definite, the curve or surface is said to be concave. (View Highlight)
- The negative of a concave function is a convex function. But the negative of a nonconvex function is again nonconvex. (View Highlight)
(View Highlight)
- Note: Third definition of convexity