Vaswani, et al. (2017)

Summary

May prove to be one of the most important scientific papers in human history. Introduces an encoder-decoder architecture that eschews recurrent neural networks in favor of multiple forms of attention (including “self-attention,” which is introduced by name in this paper). There are two key consequences to note:

(1) Self-attention provides all-vs-all position-wise semantic information to every element in the input sequence, making it possible to encode long-range associations that in turn reveal structural nuance.

(2) The pure attention model treats the output as a sort of continuation of the input sequence, which again enables a much more nuanced connection between the two.

The paper is notoriously difficult to read, for good reasons (integration of many prior concepts alongside radical innovation) and bad ones (forward references, inconsistent notation). My own attempt to describe the mechanism is here.

Attention is All You Need

Metadata

• Author: Vaswani, et al. (2017)
• Full Title: Attention is All You Need
• Category:articles
• Summary: The document introduces the Transformer, a model architecture for machine translation tasks that relies solely on attention mechanisms without recurrence or convolutions. This architecture allows for more parallelization, quicker training times, and superior quality in translation compared to existing models. By using self-attention to compute representations of input and output sequences, the Transformer achieves state-of-the-art results while being more efficient in terms of computation and training costs. The document details the model architecture, attention mechanisms, and reasons for choosing self-attention over traditional recurrent or convolutional layers.
• URL: https://arxiv.org/pdf/1706.03762.pdf

Highlights

• sequence transduction models (View Highlight)

New highlights added March 25, 2024 at 11:15 AM

• attention mechanism (View Highlight)
• Recurrent models typically factor computation along the symbol positions of the input and output sequences. Aligning the positions to steps in computation time, they generate a sequence of hidden states ht, as a function of the previous hidden state ht−1 and the input for position t. This inherently sequential nature precludes parallelization within training examples, which becomes critical at longer sequence lengths, as memory constraints limit batching across examples. (View Highlight)
• In this work we propose the Transformer, a model architecture eschewing recurrence and instead relying entirely on an attention mechanism to draw global dependencies between input and output. (View Highlight)
• For translation tasks, the Transformer can be trained significantly faster than architectures based on recurrent or convolutional layers. (View Highlight)

New highlights added April 1, 2024 at 4:20 PM

• We propose a new simple network architecture, the Transformer, based solely on attention mechanisms, dispensing with recurrence and convolutions entirely. (View Highlight)
• being more parallelizable and requiring significantly less time to train. (View Highlight)
• This inherently sequential nature precludes parallelization within training examples, which becomes critical at longer sequence lengths, as memory constraints limit batching across examples. (View Highlight)
• [27], (View Highlight)
  • Note: This paper is called “A decomposable attention model,” but I’ve never heard anyone talk about it.
• In the Transformer this is reduced to a constant number of operations, albeit at the cost of reduced effective resolution due to averaging attention-weighted positions, an effect we counteract with Multi-Head Attention as described in section 3.2. (View Highlight)
  • Note: Unlike prior art, Transformers can relate signals from any position in the sequence in constant time.
• Self-attention (View Highlight)
  • Note: I was initially confused as to how this differs from the BiRNN used in Bahdanau 2015. Bahdanau computes two state vectors for each input token and concatenates them. Since the new state incorporates “history” from upstream and downstream, each resulting hidden state associates the embedding of the current position (i.e., its meaning out-of-context) with context from the rest of the sequence, especially nearby tokens. As a result, the hidden encoder state, which they call an “annotation,” encodes both out-of-context and in-context meaning for the specific token. By comparison, self-attention computes a “compatibility score” between each position and each other position. It then computes an average of all the embeddings, weighted by compatibility. The resulting vector reflects a sort of expectation of the meaning in-context of the token at that position. When generating output tokens, the model can then dynamically adjust the weighting of each prior token according to their relevance.
• the Transformer is the first transduction model relying entirely on self-attention to compute representations of its input and output without using sequence- aligned RNNs or convolution. (View Highlight)
• Encoder and Decoder Stacks (View Highlight)
  • Note: It’s clear that this paper needs to be read twice, since concepts are defined in terms of one another.
• multi-head self-attention mechanism, (View Highlight)
  • Note: Defined below
• residual connection (View Highlight)
  • Note: A design pattern in which the input to a layer is added to its output before being passed on to the next layer. This prevents the collapse of gradients, allowing networks to become deeper without losing robustness.
• the output of each sub-layer is LayerNorm(x + Sublayer(x)), where Sublayer(x) is the function implemented by the sub-layer itself. (View Highlight)
  • Note: All of the layers HAVE to be the same size to work in this way.
• In addition to the two sub-layers in each encoder layer, the decoder inserts a third sub-layer, which performs multi-head attention over the output of the encoder stack (View Highlight)
  • Note: Decoder does multi-head attention twice

New highlights added April 1, 2024 at 5:20 PM

• We also modify the self-attention sub-layer in the decoder stack to prevent positions from attending to subsequent positions. This masking, combined with fact that the output embeddings are offset by one position, ensures that the predictions for position i can depend only on the known outputs at positions less than i. (View Highlight)

New highlights added April 2, 2024 at 11:20 AM

• An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. (View Highlight)
  • Note: This is a little bit forced compared with the original (Bahdenau) attention mechanism. In that paper, the hidden decoder state is the query, the context vector is the output, and the ‘key value pairs’ are just values: the input annotations. In the review article I read, they state that this is solved by letting the key equal the value.
• The output is computed as a weighted sum (View Highlight)
• of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key. (View Highlight)

New highlights added April 2, 2024 at 5:20 PM

• We call our particular attention “Scaled Dot-Product Attention” (Figure 2). The input consists of queries and keys of dimension dk, and values of dimension dv. We compute the dot products of the query with all keys, divide each by √ dk, and apply a softmax function to obtain the weights on the values. (View Highlight)
• (1) (View Highlight)
  • Note: : Matrix of embeddings representing the “keys” : Matrix of embedings representing the “queries” : Matrix of embeddings representing the “values” All of which are obtained by linearly projecting the attended sequence according to matrices learned during training.
• dk (View Highlight)
  • Note: Scaled by square root of the key embeddings’ dimensionality in order to prevent gradient collapse.
• Instead of performing a single attention function with dmodel-dimensional keys, values and queries, we found it beneficial to linearly project the queries, keys and values h times with different, learned linear projections to dk, dk and dv dimensions, respectively. (View Highlight)
• different representation subspaces at different positions (View Highlight)
  • Note: The phrase “at different positions” makes this needlessly confusing. The idea is that each “head” is able to learn a different aspect of the input sequence. By concatenating the “heads” into a single attention vector, the resulting vector incorporates each of the learned feature spaces, and hence reflects a more nuanced understanding of the sequence’s meaning.
• W (View Highlight)
  • Note: is a convention for a learned matrix of weights. Here these weights are used to perform a linear projection of the input sequence into the key, value, and query spaces. So we have 3*h + 1 weight matrices in play per multi-head attention layers: K, Q, and V for each head; plus W^O for projecting the concatenated result into the size of the layer (which in this paper is 512).

New highlights added April 3, 2024 at 10:20 AM

• Attention Is All You Need (View Highlight)

New highlights added April 5, 2024 at 1:18 PM

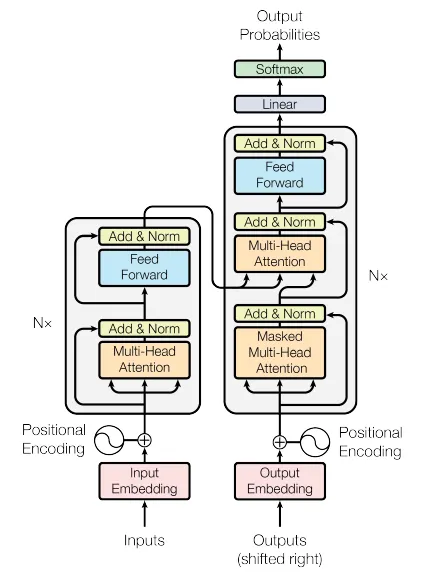
• Figure 1 (View Highlight)
  • Note: I still don’t understand exactly how the decoder works, after reading the paper and “The Illustrated Transformer.”
• multi-head (View Highlight)
• the output of each sub-layer is LayerNorm(x + Sublayer(x)), where Sublayer(x) is the function implemented by the sub-layer itself. (View Highlight)
  • Note: All of the layers HAVE to be the same size to work in this way.