Explored the idea of enhancing the text-to-speech of math-heavy books using ML. First idea was to use an image-to-latex model (of which there are many, trained on the IM2LATEX-100K dataset), and then having an LLM express the LaTeX in English. This sort-of worked, but the explanation was still pretty naive until I told it the context of the equation, at which point it injected too many assumptions.
For example, I gave it the following system of equations:
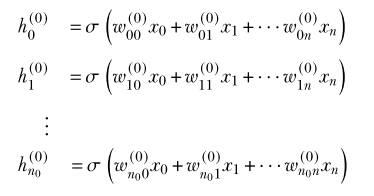 ChatGPT expressed this as:
ChatGPT expressed this as:
h subscript 0 superscript 0 equals sigma of open parenthesis w subscript 0 0 superscript 0 x subscript 0 plus w subscript 0 1 superscript 0 x subscript 1 plus dots plus w subscript 0 n superscript 0 x subscript n close parenthesis
h subscript 1 superscript 0 equals sigma of open parenthesis w subscript 1 0 superscript 0 x subscript 0 plus w subscript 1 1 superscript 0 x subscript 1 plus dots plus w subscript 1 n superscript 0 x subscript n close parenthesis
ellipsis
h subscript n subscript 0 superscript 0 equals sigma of open parenthesis w subscript n subscript 0 0 superscript 0 x subscript 0 plus w subscript n subscript 0 1 superscript 0 x subscript 1 plus dots plus w subscript n subscript 0 n superscript 0 x subscript n close parenthesis
That is not going to be comprehensible. So I asked it to note that it’s working with tensors, at which point it replied:
The first equation states that the output of the first neuron in the first layer, denoted as h sub zero superscript open paren zero close paren, is obtained by applying the activation function sigma to the weighted sum of the inputs. Specifically, this sum includes the input x sub zero multiplied by the weight w sub zero zero superscript open paren zero close paren, plus the input x sub one multiplied by the weight w sub zero one superscript open paren zero close paren, and so on, up to x sub n multiplied by the weight w sub zero n superscript open paren zero close paren.
The second equation is similar but applies to the second neuron in the first layer, denoted as h sub one superscript open paren zero close paren. Again, the output is the result of applying the activation function sigma to the weighted sum of the inputs, using the corresponding weights w sub one zero superscript open paren zero close paren, w sub one one superscript open paren zero close paren, and so on, up to w sub one n superscript open paren zero close paren.
The pattern continues in the same manner for all neurons in the first layer, up to the n sub zero-th neuron, whose output is denoted as h sub n sub zero superscript open paren zero close paren. This output is also obtained by applying the activation function sigma to the weighted sum of the inputs, using the weights w sub n sub zero zero superscript open paren zero close paren, w sub n sub zero one superscript open paren zero close paren, and so on, up to w sub n sub zero n superscript open paren zero close paren.
After telling it to answer as a mathematician from 100 years ago might, it reverted to its first representation. Finally, after reminding it that the mathematician would understand the tensor notation but not its context, it gave a satisfactory reply for the first equation:
The component h subscript zero, superscript parenthesis zero, is obtained by applying the function sigma to a linear combination of the terms. This combination includes w subscript zero zero, superscript parenthesis zero, multiplied by x subscript zero, plus w subscript zero one, superscript parenthesis zero, multiplied by x subscript one, continuing in this manner up to w subscript zero n, superscript parenthesis zero, multiplied by x subscript n.
Applying chain-of-thought reasoning by asking it to convert back to LaTeX first was also helpful. I asked it for a new prompt, and it suggested this one:
Can you describe the following system of equations as a mathematician from 100 years ago might? They should be familiar with tensor notation but not the specific modern context. The system of equations is:
So I started a new conversation, this time starting by asking it to express the equation as LaTex, which it gave as:
So far so good. I then started a new conversation, in which I gave it this prompt:
Pretend you are a highly mature mathematician from another era, fully numerate in all modern notation, but unfamiliar with domain knowledge of any applications. You are discussing with a friend some mysterious math that you found scrawled on a chalkboard. Please express in plain English, suitable for a text-to-speech system, exactly what words you would say to this friend in conversation in order to convey the equation. The math you see is equivalent to the rendered version of the following LaTeX...
It replied unhelpfully:
My friend, upon encountering this curious set of equations on the chalkboard, I found myself pondering their meaning. Here is how I would describe them in plain English:
We have a series of expressions, each beginning with an "h" followed by a subscript and superscript zero in parentheses, indicating it is part of a particular set or layer. For each of these expressions, we apply a function denoted by the Greek letter sigma, which I surmise represents some kind of transformation or activation function.
Inside each sigma function, we have a sum of terms. Each term consists of a weight, represented by a "w" with two subscripts and a superscript zero in parentheses, multiplied by a corresponding "x" variable. These "x" variables, I believe, are inputs to the system.
For example, the first equation reads as follows:
"h naught to the zero equals sigma of the sum of w naught naught to the zero times x naught, plus w naught one to the zero times x one, and so forth, up to w naught n to the zero times x n."
The pattern continues similarly for subsequent equations:
"h one to the zero equals sigma of the sum of w one naught to the zero times x naught, plus w one one to the zero times x one, and so forth, up to w one n to the zero times x n."
This pattern persists until the final equation in this series:
"h n subscript zero to the zero equals sigma of the sum of w n subscript zero naught to the zero times x naught, plus w n subscript zero one to the zero times x one, and so forth, up to w n subscript zero n to the zero times x n."
In essence, each equation is a weighted sum of the inputs, transformed by the sigma function, producing outputs "h" for some initial layer denoted by the superscript zero.
So I tried a less colorful approach:
Please express the following LaTeX in a way that a visually impaired person could follow, but without injecting any assumptions about the application domain, such that they can use it to understand the mathematical basis for whatever domain it came from. You must express it in plain words so that it can be fed into a text-to-speech tool.
This came out great:
We have a set of equations defining a series of functions, each denoted by h with different subscripts and superscripts.
The first function is: h subscript 0 superscript (0) equals the function sigma applied to the sum of several terms. Each term is a product of a weight, w, with two subscripts and a superscript (0), and a variable, x, with a subscript. Specifically, the terms are:
- w subscript 00 superscript (0) times x subscript 0,
- w subscript 01 superscript (0) times x subscript 1,
- continuing in this pattern up to
- w subscript 0n superscript (0) times x subscript n.
Thus, the first equation is: h subscript 0 superscript (0) equals sigma of the sum of these terms.
The second function is similar, but with different indices: h subscript 1 superscript (0) equals sigma of the sum of terms where each term is a product of a weight, w, and a variable, x. Specifically, the terms are:
- w subscript 10 superscript (0) times x subscript 0,
- w subscript 11 superscript (0) times x subscript 1,
- continuing in this pattern up to
- w subscript 1n superscript (0) times x subscript n.
Thus, the second equation is: h subscript 1 superscript (0) equals sigma of the sum of these terms.
This pattern continues for all functions up to: h subscript n_0 superscript (0) equals sigma of the sum of terms where each term is a product of a weight, w, and a variable, x. Specifically, the terms are:
- w subscript n_0 0 superscript (0) times x subscript 0,
- w subscript n_0 1 superscript (0) times x subscript 1,
- continuing in this pattern up to
- w subscript n_0 n superscript (0) times x subscript n.
Thus, the last equation is: h subscript n_0 superscript (0) equals sigma of the sum of these terms.
Here, sigma represents a function applied to the entire sum, and each equation follows the same structure, differing only by the subscripts on the weights and the functions.
With this in mind, I iterated with another image:
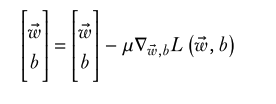 Again I started by asking it to typeset the image as LaTeX, resulting in
Again I started by asking it to typeset the image as LaTeX, resulting in
I then told it:
You are generating text from equations for text-to-speech in an assistive context for visually impaired readers. Please express the following equation in words suitable for text-to-speech.
$$
\begin{bmatrix}
\vec{w} \\
b
\end{bmatrix}
=
\begin{bmatrix}
\vec{w} \\
b
\end{bmatrix}
- \mu \nabla_{\vec{w}, b} L(\vec{w}, b)
$$
For context, the preceding paragraph is as follows:
> The error is a function of the parameter set w. The question is, how do we adjust w so that the error e2 i decreases? We know a function’s value changes most when we move along the direction of the gradient of the parameters. Hence, we adjust the parameters w, b as follows:
And the following paragraph is as follows:
Each adjustment reduces the error. Starting from a random set of parameter values and doing this a sufficiently large number of times yields the desired model.
It replied:
The equation in the text-to-speech format is:
"The vector w and scalar b are updated as follows: the vector w and scalar b are equal to the vector w and scalar b minus mu times the gradient of L with respect to w and b."
Not bad, but if it is saying “are updated as follows,” it should probably have left out “the vector w and scalar b are equal to.”
The ideal answer would probably have been “The vector w and scalar b are updated as the old vector w and scalar b minus mu times the gradient of L with respect to w and b.”